I have finally finished the tool for converting Isabelle verified IsarMathLib source to a blog entry. Writing a parser with Haskell’s Parsec library was a pleasure as usual. The post below was generated from the Fold_ZF.thy theory file that will be included in the next (1.6.2) release of IsarMathLib.
Having a parser opens the possibility of exporting the IsarMathLib source to different formats. I have been thinking what my next target should be and decided it should be TiddlyWiki.
Why TiddlyWiki?
There are two most important features that a good presentation of formalized mathematics should have.
1. Mathematical notation including mathematical symbols.
You can not effectively communicate mathematics without mathematical symbols. Most theorem provers designers seem not to understand this. It is a mystery for me why the designers of programming languages are stuck at the set of symbols that were present on those typewriters that people used to talk to IBM mainframes in the sixties. It obviously wastes the bandwith of human visual cognition channel that can recognize thousands of symbols easily and fast. Fortunately Isabelle is an exception to this – it allows to define any number of custom symbols and specify how they should be typeset in the proof document. As for TiddlyWiki the jsMath plugin allows beautiful display of LaTeX math notation, much better that what you can see in this blog.
2. Ways to deal with excessive verbosity of formalized math
Formalized proofs contain much more details than informal ones. It is good in some way that a machine will not accept proofs written in style “using methods similar to those in [1] modified in a way analogous to [2] we can show that …” . On the other hand having too much detail can make it difficult to see the main idea and the big picture of a proof. Isabelle’s Isar language allows to write structured proofs where the proofs of the main points can be can be separated in the whole proof text so they can be skipped by the reader if the fact is obvious to him/her. TiddlyWiki’s NestedSlidersPlugin would allow to expand such sub-proofs only on demand, so that they don’t obstruct the flow of the main proof.
Another aspect of verbosity of formal proofs is that they typically reference many more other theorems than a typical informal proof. It is sometimes difficult to see which of the referenced theorems are essential to understanding of the proof and which ones are only the glue logic. Isabelle allows to add some theorems to the simplifier where they effectively become the background knowledge that is not necessary to reference directly in proofs. The NestedSlidersPlugin does something even better – it can make the theorem reference clickable, so that the reader can easily examine what the referenced theorem is saying in a window floating over the main text.
And now some formalized mathematics about folding in ZF set theory.
theory Fold_ZF imports InductiveSeq_ZF
begin
Suppose we have a binary operation written multiplicatively as
. In informal mathematics we can take a sequence
of elements of
and consider the product
. To do the same thing in formalized mathematics we have to define precisely what is meant by that “
“. The definitition we want to use is based on the notion of sequence defined by induction discussed in InductiveSeq_ZF. We don’t really want to derive the terminology for this from the word “product” as that would tie it conceptually to the multiplicative notation. This would be awkward when we want to reuse the same notions to talk about sums like
.
In functional programming there is something called “fold”. Namely for a function , initial point
and list
the expression fold(f, a, [b,c,d]) is defined to be f(f(f(a,b),c),d) (in Haskell something like this is called foldl). If we write
in multiplicative notation we get
, so this is exactly what we need. The notion of folds in functional programming is actually much more general that what we need here (not that I know anything about that). In this theory file we just make a slight generalization and talk about folding a list with a binary operation
with
not necessarily the same as
.
Folding in ZF
Suppose we have a binary operation . Then every
defines a transformation of
defined by
. In IsarMathLib such transformation is called as Fix2ndVar(f,y). Using this notion, given a function
and a sequence
of elements of
we can get a sequence of transformations of
. This is defined in Seq2TransSeq below. Then we use that sequence of tranformations to define the sequence of partial folds (called FoldSeq) by means of InductiveSeqVarFN (defined in InductiveSeq_ZF theory) which implements the inductive sequence determined by a starting point and a sequence of transformations. Finally, we define the fold of a sequence as the last element of the sequence of the partial folds.
Definition that specifies how to convert a sequence of elements of
into a sequence of transformations of
, given a binary operation
.
definition
Definition of a sequence of partial folds.
definition
Definition of a fold.
definition
If is a set with a binary operation
then Seq2TransSeqN(f,a) converts a sequence
of elements of
into the sequence of corresponding transformations of
.
lemma seq2trans_seq_props:
assumes A1: 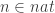 and
A2:
and
A2:  and
A3:
and
A3:  and A4:
and A4: 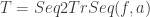 shows
shows  and
and
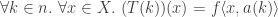 proof -
from
proof -
from  have D:
have D: 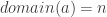 using func1_1_L1
with A2 A3 A4 show
using func1_1_L1
with A2 A3 A4 show  using apply_funtype fix_2nd_var_fun ZF_fun_from_total Seq2TrSeq_def
with A4 D have I:
using apply_funtype fix_2nd_var_fun ZF_fun_from_total Seq2TrSeq_def
with A4 D have I: 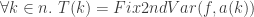 using Seq2TrSeq_def ZF_fun_from_tot_val0
{
fix
using Seq2TrSeq_def ZF_fun_from_tot_val0
{
fix  fix
fix  assume A5:
assume A5:  ,
, 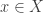 with A1 A3 have
with A1 A3 have  using apply_funtype
with A2 A5 I have
using apply_funtype
with A2 A5 I have 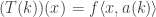 using fix_var_val
}
thus
using fix_var_val
}
thus 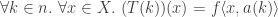 qed
qed
Basic properties of the sequence of partial folds of a sequence .
theorem fold_seq_props:
assumes A1: 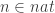 and
A2:
and
A2:  and
A3:
and
A3:  and A4:
and A4: 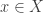 and
A5:
and
A5:  and A6:
and A6:  shows
shows 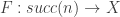 ,
, 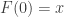 and
and
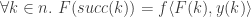 proof -
let
proof -
let  from A1 A3 have D:
from A1 A3 have D:  using func1_1_L1
from
using func1_1_L1
from 
 have I:
have I:  using fstdomdef
with A1 A2 A3 A4 A6 D show II:
using fstdomdef
with A1 A2 A3 A4 A6 D show II: 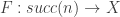 and
and 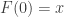 using seq2trans_seq_props FoldSeq_def fin_indseq_var_f_props
from A1 A2 A3 A4 A6 I D have
using seq2trans_seq_props FoldSeq_def fin_indseq_var_f_props
from A1 A2 A3 A4 A6 I D have  using seq2trans_seq_props FoldSeq_def fin_indseq_var_f_props
moreover {
fix
using seq2trans_seq_props FoldSeq_def fin_indseq_var_f_props
moreover {
fix  assume A5:
assume A5:  hence
hence  with A1 A2 A3 II A5 have
with A1 A2 A3 II A5 have 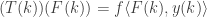 using apply_funtype seq2trans_seq_props
}
ultimately show
using apply_funtype seq2trans_seq_props
}
ultimately show 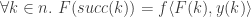 qed
qed
A consistency condition: if we make the list shorter, then we get a shorter sequence of partial folds with the same values as in the original sequence. This can be proven as a special case of fin_indseq_var_f_restrict but a proof using fold_seq_props and induction turns out to be shorter.
lemma foldseq_restrict:
assumes 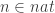 ,
,  and
and
 ,
,  ,
,
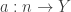 ,
, 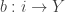 and
and
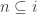 ,
,
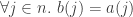 ,
, 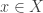 ,
,  shows
shows  proof -
let
proof -
let  let
let  from assms have
from assms have 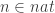 ,
,  ,
,  and
and
 using fold_seq_props
then show
using fold_seq_props
then show 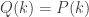 by (rule fin_nat_ind)
qed
by (rule fin_nat_ind)
qed
A special case of foldseq_restrict when the longer sequence is created from the shorter one by appending one element.
corollary fold_seq_append:
assumes 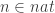 ,
,
 ,
,  and
and
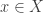 ,
,  ,
, 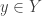 shows
shows 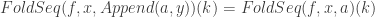 proof -
let
proof -
let  from assms have
from assms have 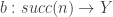 ,
, 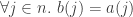 using append_props
with assms show
using append_props
with assms show 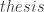 using foldseq_restrict
qed
using foldseq_restrict
qed
What we really will be using is the notion of the fold of a sequence, which we define as the last element of (inductively defined) sequence of partial folds. The next theorem lists some properties of the product of the fold operation.
theorem fold_props:
assumes A1: 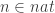 and
A2:
and
A2:  ,
,
 ,
, 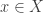 ,
,  shows
shows 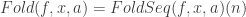 and
and  proof -
from assms have
proof -
from assms have 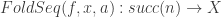 using fold_seq_props
with A1 show
using fold_seq_props
with A1 show 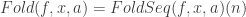 and
and  using last_seq_elem apply_funtype Fold_def
qed
using last_seq_elem apply_funtype Fold_def
qed
The next theorem tells us what happens to the fold of a sequence when we add one more element to it.
theorem fold_append:
assumes A1: 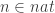 and
A2:
and
A2:  and
A3:
and
A3:  and
A4:
and
A4: 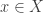 and A5:
and A5: 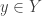 shows
shows 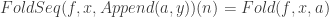 and
and
 proof -
let
proof -
let  let
let  from A5 have I:
from A5 have I:  with assms show thesis1:
with assms show thesis1: 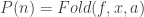 using fold_seq_append fold_props
from assms I have II:
using fold_seq_append fold_props
from assms I have II:  ,
,
 ,
, 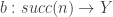 ,
,
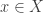 ,
,  ,
,  using append_props
then have
using append_props
then have  by (rule fold_seq_props)
with A3 A5 thesis1 have
by (rule fold_seq_props)
with A3 A5 thesis1 have  using append_props
moreover
from II have
using append_props
moreover
from II have  by (rule fold_seq_props)
then have
by (rule fold_seq_props)
then have 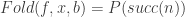 using last_seq_elem Fold_def
ultimately show
using last_seq_elem Fold_def
ultimately show  qed
end
qed
end
The formal part of this blog post has been generated from IsarMathLib’s Fold_ZF.thy theory file, see the relevant pages of the IsarMathLib proof document.
Update Sept. 19 2008: See also the TiddlyWiki rendering of this post.
Tags: proofs algebra
Leave a comment